Kondensatorinduktorberäkningar

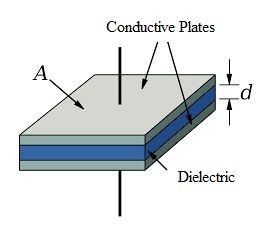
Induktorer kan föreställas som motsatsen till kondensatorer. Huvudskillnaden mellan en kondensator och en induktor är att en kondensator bär ett skyddande dielektrikum mellan sina plattor, vilket hämmar ledningen av ström över sina terminaler. Här fungerar det som en öppen krets.

Å andra sidan har induktansen hos en induktor normalt (men inte alltid) otroligt lågt eller minimalt motstånd. Det fungerar i princip som en sluten krets.

Kondensator Induktor Dualitet

Det finns en unik term inom elektronik för denna typ av förhållande mellan två parametrar i en krets eller delar av en krets. Elementen i denna typ av par är kända som dualer av varandra . Till exempel, beroende på förmågan att leda ström, är en öppen krets den dubbla av en sluten krets.

På samma princip är en induktor den dubbla av en kondensator. Dualiteten hos induktorer och kondensatorer är mycket djupare än bara den naturliga förmågan att leda ström.

I den här artikeln jämför vi arbetsprincipen för induktor och kondensator för och utvärderar resultaten med beräkningar och formler.

Trots att induktorer normalt sällan ses i elektroniska kretsar, eftersom de idag oftast ersätts av opamper i aktiva filter), verkar de andra delarna som är inblandade i en krets ha en viss mängd induktans.

Självinduktansen av terminalerna på en kondensator eller motstånd blir ett stort problem i högfrekventa kretsar, vilket förklarar varför blyfria ytmonterade motstånd och kondensatorer används så ofta i sådana applikationer.

Grundläggande kondensatorekvationer

Den grundläggande ekvationen för kondensatorer är den som farad definieras med:

C = Q / I [ekv.19]

där C är kapacitansen i farad, Q är laddningen i coulomb och U är pd mellan plattorna i volt.

Genom ekv. 19, får vi en formel av formen Q = ∫ I dt + c där c är den ursprungliga laddningen, om tillgänglig. Efter att ha identifierat Q kan vi bestämma U från ekv. 19:

U = 1 / C ∫ I dt + c / C. [Ekv.21]

En viktig egenskap hos en kondensator kan vara så här, om en periodisk ström appliceras på den (vanligtvis en ström som svänger sinusformigt), varierar laddningen på kondensatorn och spänningen över den också sinusformigt.

Laddnings- eller spänningskurvan är en negativ cosinuskurva, eller så kan vi föreställa oss den som en sinuskurva som ligger efter strömkurvan med Pi / 2-drift (90 °).

Den grundläggande ekvationen som definierar Henry, induktansenheten, är

L = NΦ / I [Ekv.22]

Med hänvisning till en enda spole kan självinduktansen i henry vara fl ux-förhållandet (den magnetiska fl ux<1) in weber multiplied by the number of winding N, (because the magnetic flux cuts through each turn), when a unit current passes through it (I = 1 A). An even more handy definition could be extracted from Eq. 22, using Neumann’s equation. This claims that:

U = N (dΦ / dt) [Ekv.23]

Vad denna ekvation antyder är det faktum att e.m.f. inducerad i en induktor är relativt den länkade förändringshastigheten på fl ux.

Ju snabbare varies ux varierar, desto högre induceras e.m.f. Till exempel när flödet över induktorn eller spolen stiger med en hastighet av 2 mWb s^-1och förutsatt att spolen har tjugofem varv, då är U = 25x2 = 50V.

Vägen till e.m.f. är sådan att den motstår de variationer i flöde som anges i Lenzs lag.

Denna sanning påpekas ofta genom att föregå den högra sidan av ekvationen med ett minustecken, men så länge vi tror att U är baksidan e.m.f., kan tecknet tas bort.

Differentialer

Termen dΦ / dt i ekv. 23 anger vad vi lärde oss som förändringshastigheten för fl ux. Uttrycket kallas differensen av Φ med avseende på t, och en hel gren av aritmetik är tillägnad att arbeta med denna typ av uttryck. Frasen har formen av ett enda nummer (dΦ) dividerat med ytterligare en kvantitet (dt).

Differentialer används för att associera många uppsättningar proportioner: dy / dx, till exempel, korrelerar variablerna x och y. När en graf ritas med värden x över den horisontella axeln och värdena y över den vertikala axeln, betyder dy / dx hur brant lutningen är eller lutningen i diagrammet.

Om U är FET-grindkällspänningen, där T är den relaterade dräneringsströmmen, betyder dI / dU mängden med vilken jag ändras för givna ändringar i U. Alternativt kan vi säga att dI / dU är trans-konduktansen. När man diskuterar induktorer kan dΦ / dt vara hastigheten på förändring av fl ux med tiden.

Beräkning av en differentiering kan betraktas som det omvänt integrationsförfarandet. Det finns inte tillräckligt med utrymme i den här artikeln för att undersöka teorin om differentiering, ändå kommer vi att definiera en tabell över vanliga kvantiteter tillsammans med deras differentier.

Standarddifferenser

Tabellen ovan fungerar genom att använda I och t som faktorer istället för rutinen x och y. Så att dess detaljer är specifikt relevanta för elektronik.

Som ett exempel, med tanke på att I = 3t +2, kan det sätt jag avviker med avseende på tid visualiseras i diagrammet i Fig. 38. För att hitta förändringshastigheten för I när som helst uppskattar vi dI / dt, genom att med hänvisning till tabellen.

Det första elementet i funktionen är 3t eller, för att formatera det som första rad i tabellen, 3t¹. Om n = 1 är differensen 3t^1-1= 3t⁰.

Sedan t⁰= 1, skillnaden är 3.

Den andra kvantiteten är 2, som kan uttryckas som 2t⁰.

Detta ändrar n = 0 och skillnaden är noll. Differensen för en konstant är alltid noll. Att få båda dessa kombinerade har vi:

dI / dt = 3

I denna illustration inkluderar inte differentialen t, det betyder att differentialen inte är tidsberoende.

Enkelt uttryckt är kurvens lutning eller lutning i fig. 38 kontinuerligt hela tiden. Figur 39 nedan visar kurvan för en annan funktion, I = 4 sin 1,5t.

Med hänvisning till tabellen är α = 1,5 och b = 0 i denna funktion. Tabellen visar, dl / dt = 4x1.5cos1.5t = 6cos 1.5t.

Detta informerar oss om den momentana förändringshastigheten för I. Till exempel vid t = 0,4, dI / dt = 6cos0.6 = 4,95. Detta kunde noteras i figur 39, där kurvan för 6 cos0.6t inkluderar värdet 4,95 när t = 0,4.

Vi kan också observera att lutningen på kurvan 4sin1.5t är 4,95 när t = 0,4, såsom visas av tangenten till kurvan vid den punkten (med avseende på de olika skalorna på de två axlarna).

När t = π / 3, en punkt när strömmen är som högst och konstant, i det här fallet dI / dt = 6cos (1,5xπ / 3): 0, vilket motsvarar nollförändring av strömmen.

Tvärtom, när t = 2π / 3 och strömmen växlar på högsta möjliga nivå från positiv till negativ, dI / dt = 6cosπ = -6, ser vi dess högsta negativa värde och uppvisar en hög strömreduktion.

Den enkla fördelen med skillnader är att de låter oss bestämma förändringshastigheter för funktioner som är mycket mer komplexa jämfört med I = 4sin 1,5t, och utan att behöva plotta kurvorna.

Tillbaka till beräkningar

Genom att omorganisera villkoren i ekv 22 får vi:

Φ = (L / N) I [Ekv.24]

Där L och N har konstanta dimensioner, men Φ och jag kan ha ett värde med avseende på tid.

Att differentiera de två sidorna av ekvationen med avseende på tid ger:

dΦ / dt = (L / N) (dI / dt) [Ekv. 25]

Att slå samman denna ekvation med ekv.23 ger:

U = N (L / N) (dI / dt) = L (dI / dt) [Ekv.26]

Detta är ett annat sätt att uttrycka Henry . Vi kan säga att en spole med självinduktans på 1 H, en strömförändring på 1 A s^-1genererar en rygg e.m.f. av 1 V. Givet en funktion som definierar hur en ström varierar med tiden, ekv. 26 hjälper oss att beräkna baksidan e.m.f. av en induktor när som helst.

Nedan följer några exempel.

A) I = 3 (en konstant ström av 3 A) dl / dt = 0. Du kan inte hitta någon förändring av strömmen därför baksidan e.m.f. är noll.

B) I = 2t (en rampström) dI / dt = 2 A s^-1. Med en spole som bär L = 0,25 H, är baksidan e.m.f. kommer att vara konstant vid 0,25 x 2 = 0,5 V.

C) I = 4sin1.5t (den sinusformade strömmen som ges i föregående illustration dl / dt = 6cos 1,5t. Med tanke på en spole med L = 0,1 H är den momentana bakre emf 0,6cos1,5t. Den bakre emf följer differentialkurvan i Fig. 39, men med amplituden 0,6 V snarare än 6 A.

Förstå 'Duals'

Följande två ekvationer betyder ekvationen för en kondensator respektive induktor:

Det hjälper oss att bestämma spänningsnivån som produceras över komponenten genom att ström varierar i tid enligt en specifik funktion.

Låt oss utvärdera det resultat som erhållits av differentierar sidorna L och H i ekv 21 med avseende på tid.

dU / dt = (1 / C) I

Som vi vet är differentiering det inversa av integration, och differentiering av ∫I dt vänder integrationen, med endast jag som resultat.

Att differentiera c / C ger noll, och omordning av termerna ger följande:

I = C.dU / dt [Ekv.27]

Detta gör det möjligt för oss att känna till strömriktningen, oavsett om den går mot kondensatorn eller kommer ut från den, som svar på en spänning som varierar beroende på en given funktion.

Det intressanta är att ovanstående kondensatorström ekvation liknar spänningsekvationen (26) för en induktor, som visar kapacitans, induktansdualitet.

På samma sätt kan ström- och potentialskillnaden (pd) eller förändringshastigheten för ström och pd vara dubbla när de appliceras på kondensatorer och induktorer.

Låt oss nu integrera ekv.26 med avseende på tid för att slutföra ekvationskvatret:

∫ U dt + c = LI

Integralen av dI / dt är = I, vi ordnar om uttrycken för att få:

I = 1 / L∫ U dt + e / L

Detta ser återigen ut ganska lik Eq.21, vilket ytterligare bevisar den dubbla karaktären hos kapacitans och induktans, och deras pd och ström.

Nu har vi en uppsättning av fyra ekvationer som kan användas för att lösa kondensator- och induktorrelaterade problem.

Till exempel kan ekv.27 användas för att lösa problemet som det här:

Problem: En spänningspuls applicerad över en 100uF ger en kurva som visas i figuren nedan.

Detta kan definieras med hjälp av följande bitvisa funktion.

Beräkna strömmen som går genom kondensatorn och plotta motsvarande grafer.

Lösning:

För det första steget använder vi ekv.27

I = C (dU / dt) = 0

För det andra fallet där U kan stiga med en konstant hastighet:

I = C (dU / dt) = 3C = 300μA

Detta visar en konstant laddningsström.

För det tredje steget när U faller på ett exponentiellt sätt:

Detta indikerar ström som flyter bort från kondensatorn i en exponentiell minskande hastighet.

Fasförhållande

I figuren Abobe appliceras en alternerande pd på en induktor. Denna pd kan när som helst uttryckas som:

Där Uo är toppvärdet för pd. Om vi ​​analyserar kretsen i form av en slinga och tillämpar Kirchhoffs spänningslag medurs får vi:

Eftersom strömmen är sinusformad här måste termerna inom parentes dock ha värdet lika med toppströmmen Io, därför får vi äntligen:

Om vi ​​jämför ekv.29 och ekv.30 finner vi att strömmen I och spänningen U har samma frekvens, och jag ligger efter U med π / 2.

De resulterande kurvorna kan studeras i följande diagram:

C

Detta visar det kontrasterande förhållandet mellan kondensator och induktor. För en induktorström sänks potentialskillnaden med π / 2, medan för en kondensator leder strömmen pd. Detta visar ännu en gång den dubbla karaktären hos de två komponenterna.